What's Actually on the AMC 10: A Complete Topic Breakdown

AMC 10 is a real step up from AMC 8. If you're preparing for it, you need to know exactly what you're walking into.
Here's the full breakdown.
The Short Version
AMC 10 covers high school math through 10th grade—Algebra I, Geometry, and parts of Algebra II. No trigonometry. No calculus. But don't let that fool you. The problems require creative thinking and combining concepts in ways school math rarely asks for.
25 questions in 75 minutes. That's 3 minutes per problem on average, but later questions can take much longer.

Test Basics
| Item | Details |
|---|---|
| Questions | 25 |
| Time | 75 minutes |
| Format | Multiple choice (5 options) |
| Eligibility | Grade 10 and below, under 17.5 years old |
| Test Dates | Every November (A and B versions) |
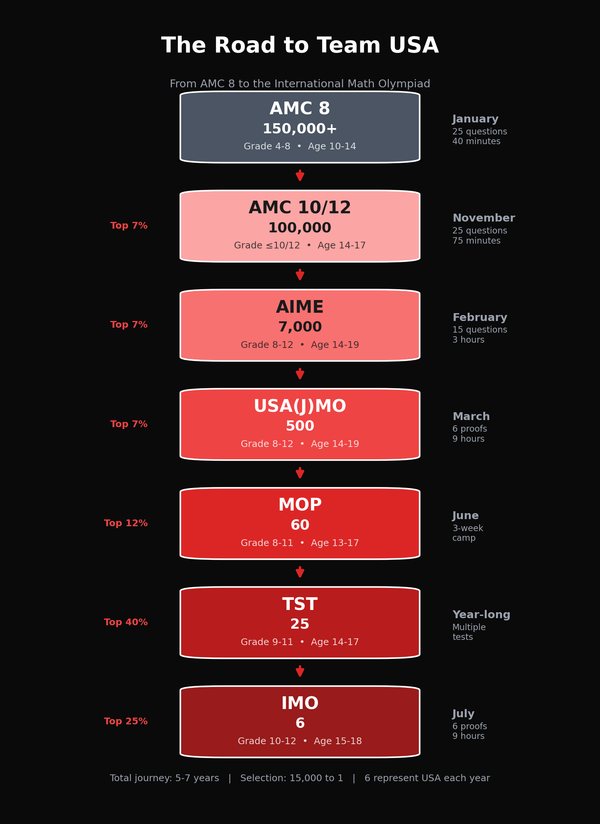
| AIME Qualification | Top ~2.5% |
The Four Main Areas
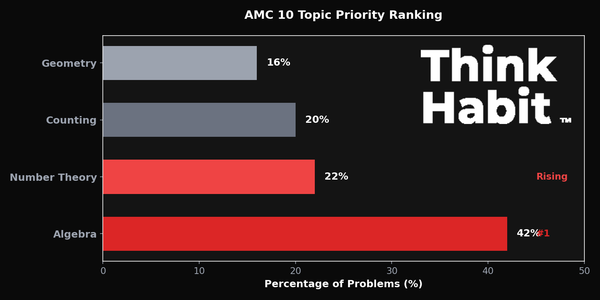
| Category | Approximate Weight |
|---|---|
| Algebra | ~35% |
| Geometry | ~30% |
| Number Theory | ~20% |
| Counting & Probability | ~15% |
These percentages shift slightly each year, but all four areas always show up heavily.
1. Algebra
Algebra is the biggest topic on AMC 10. It's also where school math and competition math differ most.

Core concepts:
- Linear equations and inequalities
- Quadratic equations and the quadratic formula
- Systems of equations (two and three variables)
- Factoring techniques
- Polynomials (roots, coefficients, factoring)
- Vieta's formulas
- Functions and their graphs
- Arithmetic and geometric sequences
- Exponents and radicals
- Absolute value equations and inequalities
- Word problems (rate, work, mixture, age)
Competition-level concepts:
- Manipulating complex algebraic expressions
- Symmetric functions
- Telescoping series
- Floor and ceiling functions
- Basic functional equations
2. Geometry
Geometry on AMC 10 goes well beyond the school curriculum. You need both computational skills and creative insight.

Core concepts:
- Triangle properties (similarity, congruence, special triangles)
- Pythagorean Theorem and its converse
- Area formulas for all standard shapes
- Circle properties (central angles, inscribed angles, tangent lines)
- Polygon properties (regular polygons, diagonals)
- Coordinate geometry (distance, midpoint, slope)
- 3D geometry (surface area, volume)
Competition-level concepts:
- Power of a point
- Cyclic quadrilaterals
- Similar triangle ratios
- Stewart's Theorem
- Mass points
- Geometric probability
- Transformations (rotation, reflection, translation)
3. Number Theory
Number theory barely exists in school curriculum, but it's a major part of AMC 10. You need dedicated study here.

Core concepts:
- Divisibility rules
- Prime factorization
- GCD and LCM
- Modular arithmetic
- Properties of remainders
- Perfect squares, cubes, and powers
- Digits and place value
Competition-level concepts:
- Euler's totient function (basics)
- Number of divisors and sum of divisors
- Diophantine equations (simple cases)
- Base number systems
- Fermat's Little Theorem (basic applications)
4. Counting & Probability
This section rewards systematic thinking. Careless mistakes are common here.
Core concepts:
- Fundamental counting principle
- Permutations and combinations
- Probability of single and compound events
- Complementary counting
- Casework
Competition-level concepts:
- Inclusion-exclusion principle
- Stars and bars
- Expected value
- Geometric probability
- Recursion in counting
- Pigeonhole principle
AMC 8 vs AMC 10: Key Differences
| AMC 8 | AMC 10 | |
|---|---|---|
| Algebra | Pre-algebra, basic equations | Full Algebra I & II, Vieta's formulas |
| Geometry | Pythagorean Theorem, basic properties | Coordinate geometry, 3D, advanced properties |
| Number Theory | Divisibility, primes, GCD/LCM | Modular arithmetic, Diophantine equations |
| Counting | Basic counting, simple probability | Inclusion-exclusion, expected value |
| Difficulty | Problems 1-15 approachable for most | Only 1-10 approachable without preparation |

Click the link below for more information on the AMC 8.
What's NOT on AMC 10
This matters too:
- Trigonometry (no sin, cos, tan)
- Logarithms (beyond very basic)
- Complex numbers
- Calculus
- Matrices
- Advanced statistics
These are AMC 12 territory.
The Real Challenge
Here's what catches most students off guard.
AMC 10 topics overlap heavily with school math. But the problems don't feel like school problems at all. A typical AMC 10 question might require:
- Figuring out which concepts even apply (it's not obvious)
- Combining two or three different areas
- Finding a creative shortcut
- Avoiding traps set by the problem writers
Knowing the formulas is necessary but not sufficient. You need to practice applying them in unexpected ways.
School Math vs AMC 10
| School Math | AMC 10 |
|---|---|
| Learn concept → Practice similar problems → Apply same method | See unfamiliar problem → Figure out which concepts → Combine creatively |
| "Use this formula to solve" | "Figure out what to use first" |
| Follow the steps, get the answer | Create the steps yourself |
AMC 10 doesn't test whether you know math. It tests whether you can think with math.
I'm a math coach at Think-Habits, and this is what I care about most. Going forward, I'll be sharing how AMC can help develop the problem-solving abilities that truly matter in the age of AI. My goal is to help you build the kind of thinking that will make a real difference in the world you're about to step into.
— Madison Chung